Аналіз обсягів бюджетного відшкодування податку з доходів фізичних осіб за допомогою багатофакторної регресійної моделі

Рис. 2.14 Матриця парних кореляцій

Таким чином, між парами факторів Х1 та Х2, Х1 та Х3 є сильний кореляційний зв'язок, що свідчить про неадекватність побудованої моделі.

Перевіримо модель на мультиколінеарність - лінійну залежність між двома або більше змінними (рис. 2.15).

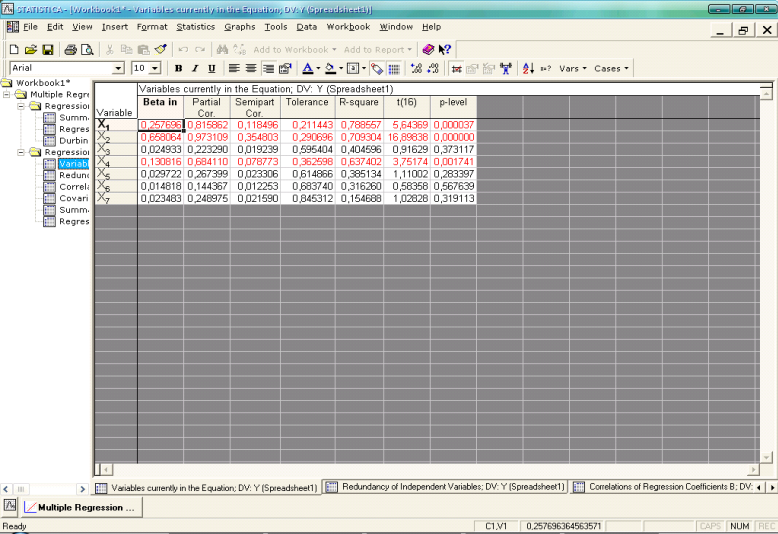
Рис. 2.15 Перевірка побудованої моделі на мультиколеніарність

Оскільки показник Tolerance для фактора Х7 перевищує граничне значення 0,8, то можна сказати, що в побудованій моделі присутня мультиколеніарність.

Проведемо аналіз моделі на автокореляцію за допомогою критерію Дарбіна-Уотсона. Автокореляція - це взаємозв’язок послідовних елементів часового чи просторового ряду даних [36]. Результати подано на рис. 2.16.

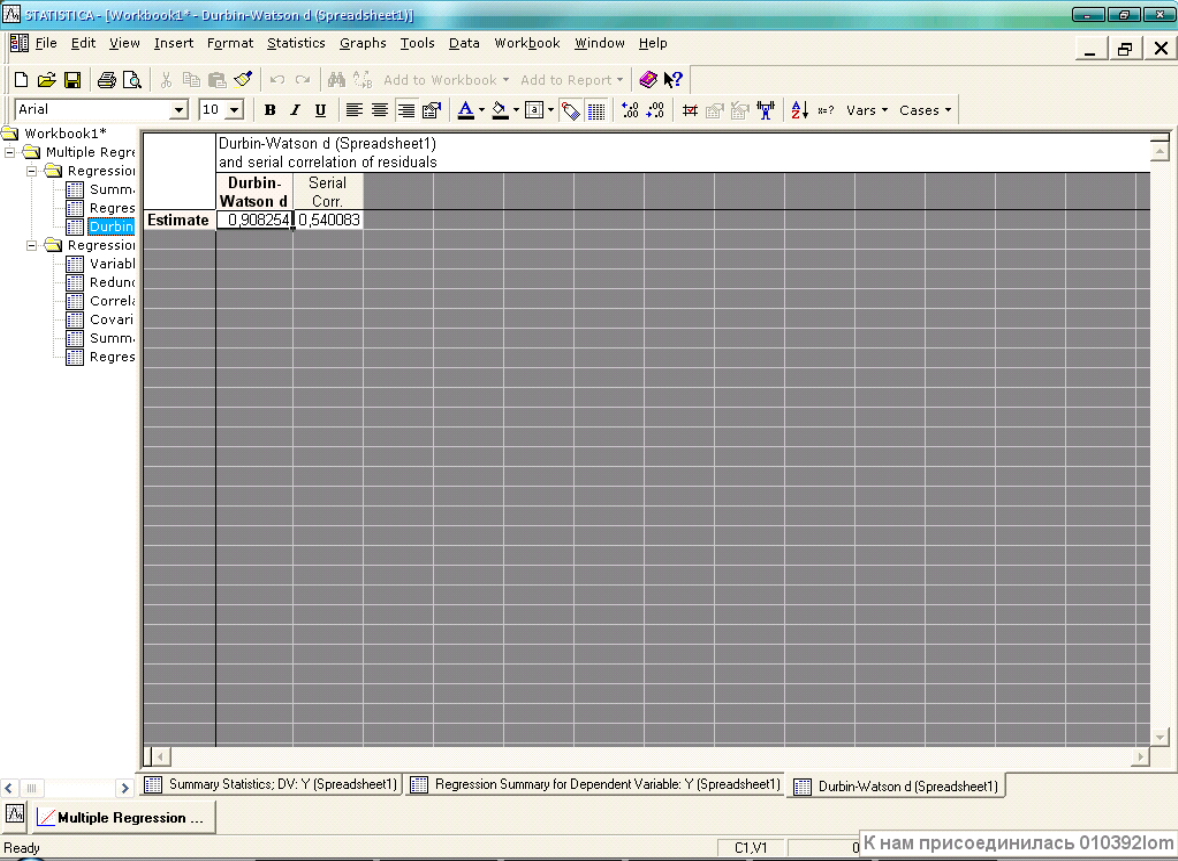
Рис. 2.16 Критерій Дарбіна-Уотсона

Якщо DW > DW1табл (DW1табл = 0,78) або DW > 4 - DW1табл, то в моделі присутня від’ємна або позитивна автокореляція відповідно. Якщо DW2табл > DW > DW1табл (DW2табл = 1,86), то критерій не дозволяє зробити висновок про наявність автокореляції. Якщо DW2табл < DW < 4 - DW2табл, то автокореляція відсутня [42]. Таким чином, можна зробити висновок, що між залишками побудованої моделі існує від’ємна автокореляція.

Перевіримо модель на адекватність за допомогою аналізу залишків моделі. Для цього побудуємо гістограму розподілу залишків (рис. 2.17).

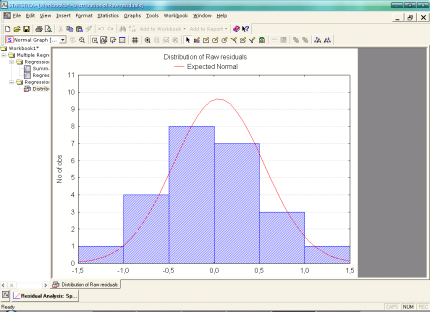
Рис. 2.17 Гістограма розподілу залишків

Гістограма розподілу залишків свідчить про те, що залишки розподілені за нормальним законом, оскільки спостерігається незначна варіація між залишками. Побудуймо графік залишків на нормальному ймовірнісному папері (рис. 2.18).

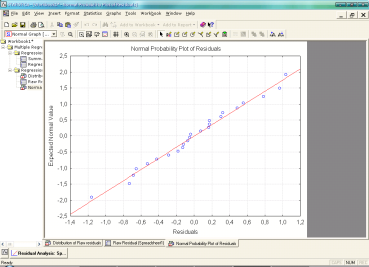
Рис. 2.18 Графік залишків на нормальному ймовірнісному папері

Графік залишків свідчить, що залишки недостатньо щільно розподілені вздовж прямої, тому не підтверджують адекватність моделі.

У зв'язку з цим, необхідно покращити модель шляхом виключення незначимих факторів Х3, Х5, Х6, Х7 з моделі. Покращимо модель методом виключень Backward stepwise. На першому кроці будується модель залежності результативної змінної від усіх заданих факторних змінних. Далі на кожному кроці виключаються фактори, які неістотно впливають на результативну змінну. Виключення проводиться доти, поки в моделі не залишаться тільки значущі факторні змінні або не буде задане значення коефіцієнта множинної кореляції (0,95) [32]. Результати покращення моделі методом виключень наведено на рис. 2.19.

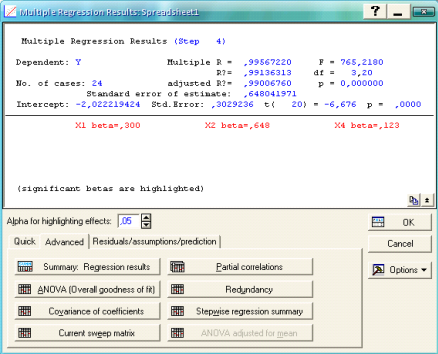
Рис. 2.19 Результати покращення моделі методом виключень

Оскільки коефіцієнт множинної кореляції Multiple R = 0,9957, то між Y та Х1, Х2, Х4 існує достатньо тісний зв'язок. Коефіцієнт детермінації R2 = 0,9914 свідчить про те, що варіація залежної змінної залежить від факторів, які були відібрані для побудови регресійної моделі. Розраховане значення критерію Фішера F = 765,218 більше Fтабл = 3,8, що свідчить, що модель є адекватною.

Читайте більше

Державний бюджет як інструмент державного регулювання економіки
Провідне місце в системі регулювання економіки держави, створення сприятливого фінансового середовища для швидкого розвитку ринкових відносин, забезпечення макроекономічної рівноваги в економіці належить бюджету. Державний бюджет представляє собою річний план державних видатків і джере ...

Механізм активізації трудової діяльності в умовах ринкової економіки
Розвиток ринкових відносин в Україні передбачає формування нової системи мотивації праці, яка враховує кардинальні зміни відносин власності, економічного статусу працівників, джерел, рівня, складу і структури їх доходів. Процес становлення ринкового механізму активізації т ...